nmmn package

Submodules

nmmn.astro module

Astrophysical routines

class nmmn.astro.Constants

Bases: object

Defines a set of useful constants in CGS.

const=nmmn.astro.Constants()
E=mass*const.c**2

nmmn.astro.arcsec2pc(d=15.0, a=1.0)

Given the input angular size and distance to the object, computes the corresponding linear size in pc.

Parameters:

• d – distance in Mpc

• a – angular size in arcsec

Returns:

linear size in pc

nmmn.astro.dist2z(d)

Converts luminosity distance to redshift by solving the equation ‘d-z=0’.

Input is assumed float.

nmmn.astro.freq(T)

Convert array of periods in days to frequencies in Hz.

nmmn.astro.mjy(lognu, ll, dist, llerr=None)

Converts log(nu/Hz), log(nu Lnu [erg/s]), error in log(nuLnu) to log(lambda/micron), log(Fnu/mJy), error in log(Fnu). The input units are CGS.

Usage: If you have errors in the flux:

>>> lamb,fnu,ferr=mjy(xdata,ydata,dist,yerr)

If you do not have errors in the flux:

>>> lamb,fnu=mjy(xdata,ydata,dist)

Parameters:

dist – distance in Mpc

nmmn.astro.period(freq)

Convert array of frequencies to periods.

nmmn.bayes module

Methods for dealing with Bayesian statistics

e.g. priors, posteriors, joint density plots.

Right now the module is focused around PyMC, but I am migrating to emcee.

Todo

plot confidence/credibility interval of a model

nmmn.bayes.allplot(xb, yb, bins=30, fig=1, xlabel='x', ylabel='y')

Input: X,Y : objects referring to the variables produced by PyMC that you want to analyze. Example: X=M.theta, Y=M.slope.

Inherited from Tommy LE BLANC’s code at astroplotlib|STSCI.

nmmn.bayes.joint_density(X, Y, bounds=None)

Plots joint distribution of variables. Inherited from method in src/graphics.py module in project git://github.com/aflaxman/pymc-example-tfr-hdi.git

nmmn.bayes.jointplotx(X, Y, xlabel=None, ylabel=None, binsim=40, binsh=20, binscon=15)

Plots the joint distribution of posteriors for X1 and X2, including the 1D histograms showing the median and standard deviations. Uses simple method for drawing the confidence contours compared to jointplot (which is wrong).

The work that went in creating this method is shown, step by step, in the ipython notebook “error contours.ipynb”. Sources of inspiration: - http://python4mpia.github.io/intro/quick-tour.html

Usage: >>> jointplot(M.rtr.trace(),M.mdot.trace(),xlabel=’$log r_{rm tr}$’, ylabel=’$log dot{m}$’)

nmmn.dsp module

Signal processing

Mostly time series.

nmmn.dsp.cwt(t, sig)

Given the time and flux (sig), this method computes a continuous wavelet transform (CWT).

Warning

Deprecated.

nmmn.dsp.cwt_spectra(t, var, dj=0.01, n=200, thres=0.1)

Computes CWT power spectrum, find peaks, produces arrays for plotting images showing the spectral lines. Note that the CWT power spectrum is an average from the CWT power array. Therefore, they are a smoothed out version of a Fourier spectrum.

Parameters:

• t – array of times

• var – array of signal

• n – number of vertical elements in image that will be created showing spectral lines

• thres – threshold parameter for finding peaks in time series

Usage: N,P,l,pp,power=cwt_spectra(t,y,thres=0.3)

Returns the following variables:

• N: 2d number of vertical elements for plotting the spectra

• P: 2d periods

• l: 2d power spectra for plotting images

• pp: periods corresponding to peaks (peak period) in power spectrum

• power: peaks in CWT power spectrum

nmmn.dsp.dt(t)

Computes difference between consecutive points in the time series.

Parameters:

• t – input times

• y – input y-values

nmmn.dsp.error_resampler(errors)

For use with pandas.

Method for performing the proper mean resampling of the uncertainties (error bars) in the time series with pandas. Note that doing a simple resampling will fail to propagate uncertainties, since error in the mean goes as

\[\sigma=\sqrt{\Sigma_n \sigma_n^2}\]

Example: Resamples the errors with 30 day averages:

# df['errflux'] has the 1sigma uncertainties
err=df['errflux'].resample('30d').apply(nmmn.dsp.error_resampler) 

# plot y-values (df['flux']) with errors (err)
df['flux'].resample('30d').mean().plot(yerr=err)

nmmn.dsp.ls(t, z, plot=False)

Computes and plot Lomb-Scargle periodogram for a given timeseries. Returns arrays with periods and LS spectral power.

>>> p,power=l.ls(time,values,plot=False)

Returns:

periods, spectral power

nmmn.dsp.ls_spectra(t, var, n=200, thres=0.1, smooth=0)

Computes Lomb-Scargle power spectrum, find peaks, produces arrays for plotting images showing the spectral lines.

Parameters:

• t – array of times

• var – array of signal

• n – number of vertical elements in image that will be created showing spectral lines

• thres – threshold parameter for finding peaks in time series

• smooth – number of points in the smoothing window. If 0, no smoothing

Usage: N,P,l,pp,power=ls_spectra(t,y,thres=0.3)

Returns the following variables:

• N: 2d number of vertical elements for plotting the spectra

• P: 2d periods

• l: 2d power spectra for plotting images

• pp: periods corresponding to peaks (peak period) in power spectrum

• power: peaks in power spectrum

nmmn.dsp.peaks(y, x=None, what=0, **args)

Detects the peaks in the time series given by Y (and X if provided).

Parameters:

• x,y – time series input arrays

• what – select what you want – max/0 or min/1 peaks returned

Returns:

xmax,ymax – arrays with max peaks in the data.

nmmn.dsp.reconstruct(wa, i=None)

Method to reconstruct a time series (TS) signal based on its CWT.

Parameters:

• wa – wavelet object generated with wavelets module

• i – index array containing only the elements that will be excluded from the signal reconstruction. i.e. the elements indicated by i will zeroed in the CWT complex array.

Returns:

full reconstructed TS, reconstructed CWT power array, reconstructed CWT complex array, detrended reconstructed TS

Examples:

1. Compute the CWT for TS in var:

import wavelets

# compute CWT
wa = wavelets.WaveletAnalysis(var, dt=dt)

# time and period 2D arrays
T, S = numpy.meshgrid(wa.time, wa.scales)

2. Reconstruct the signal, throwing out all periods with values between 1000 and 2000:

j=where((S<1000) | (S>2000))
recdet,rec=nmmn.dsp.reconstruct(wa,j)

3. Plots the reconstructed signal along with the data:

subplot(2,1,1)
plot(t,flux,label='original')
plot(t,rec,label='reconstructed signal',lw=5)

subplot(2,1,2)
plot(t,recdet,'r')
title('Pure reconstructed signal')

nmmn.dsp.reconstruct_period(wa, P1, P2)

Returns reconstructed detrended signal from CWT, considering only the interval between the two given periods.

nmmn.dsp.smooth(x, window_len=11, window='hanning')

Smooth the data using a window with requested size. Copied from http://wiki.scipy.org/Cookbook/SignalSmooth

This method is based on the convolution of a scaled window with the signal. The signal is prepared by introducing reflected copies of the signal (with the window size) in both ends so that transient parts are minimized in the begining and end part of the output signal.

Parameters:

• x – the input signal

• window_len – the dimension of the smoothing window; should be an odd integer

• window – the type of window from ‘flat’, ‘hanning’, ‘hamming’, ‘bartlett’, ‘blackman’ flat window will produce a moving average smoothing.

Returns:

the smoothed signal

Example

>>> t=linspace(-2,2,0.1)
>>> x=sin(t)+randn(len(t))*0.1
>>> y=smooth(x)

See also

numpy.hanning, numpy.hamming, numpy.bartlett, numpy.blackman, numpy.convolve, scipy.signal.lfilter

Note

length(output) != length(input), to correct this: return y[(window_len/2-1):-(window_len/2)] instead of just y.

Todo

the window parameter could be the window itself if an array instead of a string

nmmn.dsp.smoothxy(x, y, *arg, **args)

Parameters:

• x – “time” in the time series

• y – y variable

Returns:

smoothed y and corresponding x arrays

nmmn.dsp.sumts(t1, t2, y1, y2, n=1)

Given two time series, this method returns their sum.

n = number of points in the final TS, as a multiple of the sum of points in both TS.

Steps:

1. defines a uniform t-array with the number of total elements of the two arrays

2. interpolates both TS in this new t-array

3. sums their values

nmmn.dsp.uneven2even(t, y)

Given an uneven timeseries (TS) with multiple values defined at the same time, this method will convert it into an evenly sampled timeseries with a dt as close as possible to the actual dt, removing duplicate-t values.

Example: suppose you want to compute the CWT for an unevenly sampled time series. Since the CWT does not support uneven TS, you can first call this method to regularize your TS and then perform the TS.

Algorithm:

• REMOVE DUPLICATE times

• CREATE REGULAR GRID USING BEST DT

• INTERPOLATE NEW TS ON PREVIOUS ONE

Parameters:

• t – input times

• y – input value

nmmn.dsp.varsig(f, df)

Quantifies significance of variability of time series, taking into account the uncertainties.

Given the time series signal y and the corresponding uncertainties \(\sigma y\), the test statistics T is defined as

\[T \equiv \frac{y_{i+1}-y_i}{\sigma y_i}.\]

T will give the significance of variability at each point in time, in standard deviations of the preceding noise point.

Usage:

Computes TS and plots time series, highlighting the 1sigma variability interval in gray:

>>> ts=varsig(flux,errflux)
>>> step(t,q,'o-')
>>> fill_between(t, -2*ones_like(tdec), 2*ones_like(tdec), alpha=0.3, facecolor='gray')

Todo

generalize to arbitrary windows of time

Todo

propagate uncertainty

nmmn.fermi module

Methods to handle Fermi LAT data

Handle output of Fermi analysis.

nmmn.fermi.PixelFile(i, j)

return the name of a file where the result of 1 pixel evaluation will be stored

From enrico/tsmap.py.

nmmn.fermi.converttime(y)

Converts from MET Fermi time to a python datetime tuple.

>>> convertyear(386817828)

returns datetime.datetime(2013, 4, 5, 1, 23, 48).

Parameters:

y – a float or array of floats

Returns:

a datetime structure (or list) with the date corresponding to the input float or array

y is the amount of seconds since 2001.0 UTC. Beware that my method may assume that all years have 365 days.

References:

• http://stackoverflow.com/questions/19305991/convert-fractional-years-to-a-real-date-in-python

• http://heasarc.gsfc.nasa.gov/cgi-bin/Tools/xTime/xTime.pl

nmmn.fermi.getconfig(configfile='analysis.conf')

Reads config file and gets parameters.

nmmn.fermi.plotMap(counts, out='tmp.png', cmap=None, roi=None)

This method plots some count map. Inherited from the method plotMaps above.

Parameters:

• counts – FITS file with counts to be plotted

• cmap – desired colormap for image

• roi – DS9 region file if present, otherwise leave None

• out – output filename and format

Returns:

image file ‘tmp.png’ in the source folder.

nmmn.fermi.plotMaps(configfile='analysis.conf', cmap=None)

Given the directory where the results of an Enrico analysis are located (enrico_sed), this method plots the different count maps (observed, model and residuals).

This is the fixed version of the script plotMaps.py from the Enrico distribution.

Parameters:

configdir – directory with “/” at the end that points to the place

where Enrico output files are located. :returns: image file SOURCE_Maps.png in the source folder.

nmmn.fermi.plotTSmap(configfile='analysis.conf')

From Enrico/tsmap.py.

Gather the results of the evaluation of each pixel and fill a fits file

nmmn.fermi.starttime(t)

Fixes the start time of observations taken with LAT. This assumes that the time array in your light curve is in days already, and the beginning of your analysis coincides with t0 for LAT.

Parameters:

t – array with input times given in days, with t0 coinciding with the beginning of LAT

Returns:

t (days), t (years)

nmmn.grmhd module

Dealing with (GR)(R)(M)HD simulations

• RAISHIN

• Pluto

• HARM

See jupyter notebooks “grmhd*” for examples on how to use this module.

TODO:

• [ ] incorporate Pluto class from pluto-tools

• [ ]

class nmmn.grmhd.Harm(dump=None, gdump='gdump')

Bases: object

Class that reads a HARM dump datafile and converts to numpy format for plotting with matplotlib, mayavi etc. Heavily inspired/copied from harm_script.py.

Reads data from a harm dump file:

>>> d=nmmn.grmhd.Harm("dump019")

The d object will then have several attributes related to the dump physical fields, grid and coordinate information.

Inspect densities:

>>> d.rho

Convert arrays to cartesian coordinates for plotting with matplotlib:

>>> rhonew,x,y=o.cartesian(o.rho)
>>> pcolormesh(x,y,log10(rhonew))

cartesian(myvar=None)

Computes cartesian coordinates.

Arguments:

• k: 3D slice (if applicable)

cartesian_sasha(yourvar, k=0, xy=1, xcoord=None, ycoord=None, symmx=0, mirrorx=0, mirrory=0)

This was adapted from plc at harm_script.py, atchekho/harmpi. Need to understand this better.

• k: 3D slice (if applicable)

data_assign(gd, type=None, **kwargs)

dump_assign(gd, **kwargs)

fdump_assign(gd, **kwargs)

gdump2_assign(gd, **kwargs)

gdump_assign(gd, **kwargs)

rdump_assign(gd, **kwargs)

read_body(dump, nx=None, ny=None, nz=None, noround=False)

read_file(dump, type=None, savedump=True, saverdump=False, noround=False)

High-level function that reads either MPI or serial gdump’s

read_header(dump, issilent=True, returnheaderline=False)

Read the header for the dump file

class nmmn.grmhd.Raishin

Bases: object

Class that reads a RAISHIN VTK datafile and converts to numpy format.

Attributes of the object:

• x,y,z: 1D position arrays for the mesh

• rho: 1D density array

• vx,vy,vz: 1D velocity arrays

• p: 1D pressure

• bx,by,bz: 1D magnetic field arrays

• b2: 1D B^2

Define an empty object:

>>> o=nmmn.grmhd.Raishin()

Reads data from a VTK file, new attributes rho, p, vx, bx etc:

>>> o.vtk("ok200.vtk")

Saves data as an ASCII file with columns corresponding to variables:

>>> o.savetxt("ok200.dat")

regrid(var, nboost=5)

Regrid one specific RAISHIN array to a nice cartesian grid for plotting with python. Note that RAISHIN’s output is already in cartesian coordinates.

Parameters:

• var – array to be regridded e.g. d.rho

• nboost – factor of increase of number of grid points compared to previous grid

Usage:

>>> d=nmmn.grmhd.Raishin()
>>> d.vtk('ok100.vtk')
>>> d.regrid(d.rho)

TODO: - 3D version - parallel version

regridAll(nboost=5)

Regrid all RAISHIN data to a nice cartesian grid for plotting with python.

Parameters:

nboost – factor of increase of number of grid points compared to previous grid

Usage:

>>> d=nmmn.grmhd.Raishin()
>>> d.vtk('ok100.vtk')
>>> d.regridAll()

Gets interpolated rho:

>>> print(d.xc)

TODO: - 3D version - parallel version

regridsome(listarr, nboost=5)

Regrid the selected arrays in the RAISHIN data to a nice cartesian grid for plotting with python. Regridding only some of the arrays will, of course, speed up things.

Parameters:

• listarr – list of strings specifying the arrays to be regridded. Options are: rho, p, v, b

• nboost – factor of increase of number of grid points compared to previous grid

Usage:

>>> d=nmmn.grmhd.Raishin()
>>> d.vtk('ok100.vtk')
>>> d.regridsome(['rho','v'])

TODO: - 3D version - parallel version

savehdf5(outfile)

Exports data as compressed HDF5. 7x less space than ASCII.

savenumpy(outfile)

Save data as binary Numpy file .npz. 3x less space than ASCII.

savetxt(outfile)

Saves data as ASCII file

vtk(vtkfile)

Given a VTK file created with the RAISHIN GRMHD code, this reads the data as numpy arrays.

yt2d()

Converts 2d arrays from raishin to the 3d format that is understood by the yt package. Make sure you used regridAll first.

Inspired by this example: http://stackoverflow.com/questions/7372316/how-to-make-a-2d-numpy-array-a-3d-array

nmmn.grmhd.fixminus(x)

Replace nonphysical, negative values in array x with the corresponding positive numerical values. Returns modified array. Does not touch original array.

nmmn.grmhd.mdot(a, b)

Computes a contraction of two tensors/vectors. Assumes the following structure: tensor[m,n,i,j,k] OR vector[m,i,j,k], where i,j,k are spatial indices and m,n are variable indices.

nmmn.grmhd.myfloat(f, acc=1)

acc=1 means np.float32, acc=2 means np.float64

nmmn.grmhd.regridFast(self, n=None, xlim=None)

Transforms a mesh in arbitrary coordinates (e.g. nonuniform elements) into a uniform grid in the same coordinates. Uses a C function to speed things up.

One has to be particularly careful below about using a polar angle (-pi/2<theta<pi/2) vs a spherical polar angle (0<theta_sph<pi). The choice can affect some specific transformations.

Parameters:

• n – New number of elements n^2. If None, figures out by itself

• xlim – Boundary for the plot and the grid

nmmn.grmhd.wolframplot(infile, outfile, script='/Users/nemmen/work/software/mathematica/raishin.wl')

Makes a pretty plot of density field and B vector field of RAISHIN data using the Wolfram Language.

Make sure you point to the appropriate Wolfram script.

• infile: input RAISHIN ASCII file generated with Raishin.vtk above, e.g. ok200.dat

• outfile: format that will produced, e.g. ok200.png

nmmn.lsd module

LSD operations = lists, sets, dictionaries (and arrays)

nmmn.lsd.allEqual(x)

Check if all elements in an array are equal.

nmmn.lsd.arrAvg(alist)

Given a list of 1D or 2D arrays, this method computes their average, returning an array with the same shape as the input.

Parameters:

alist – list of arrays

Returns:

average, std. dev. – arrays with the same shape as the input arrays

Usage:

>>> avg=arrAvg([x,y,z])

nmmn.lsd.bootstrap(v)

Constructs Monte Carlo simulated data set using the Bootstrap algorithm.

Usage:

>>> bootstrap(x)

where x is either an array or a list of arrays. If it is a list, the code returns the corresponding list of bootstrapped arrays assuming that the same position in these arrays map the same “physical” object.

Rodrigo Nemmen, http://goo.gl/8S1Oo

nmmn.lsd.cmset_and(x, y)

Usage:

>>> cmset_and(x,y)

returns the index of the elements of array x which are also present in the array y.

This is equivalent to using the IDL command

>>> botha=cmset_op(namea, 'AND', nameb, /index)

i.e. performs the same thing as the IDL routine cmset_op.

nmmn.lsd.cmset_not(x, y)

Usage:

>>> cmset_not(x,y)

returning the index of the elements of array x which are not present in the array y.

This is equivalent to using the IDL command SET = CMSET_OP(A, ‘AND’, /NOT2, B, /INDEX) ; A but not B i.e. performs the same thing as the IDL routine cmset_op from http://cow.physics.wisc.edu/~craigm/idl/idl.html.

nmmn.lsd.cmsetsort_and(x, y)

Usage:

>>> cmsetsort_and(x,y)

returning the index of the elements of array x which are also present in the array y.

The resulting elements have the same order as the ones in y. For instance, if you run

>>> i=cmsetsort_and(x,y)
>>> x[i]==y

will return an array of True, whereas if you used instead cmset_and it is not guaranteed that all elements would match in x[i] and y.

Inherited from nemmen.cmset_and().

nmmn.lsd.crop(z, x, y, xmin, xmax, ymin, ymax, all=False)

Crops the image or 2D array, leaving only pixels inside the region you define.

>>> Znew,Xnew,Ynew = crop(Z, X, Y, 0,10,-20,20)

where X,Y are 1D or 2D arrays, and Z is a 2D array.

Parameters:

• z – 2d array

• x,y – 1d or 2d arrays. In the latter case, they should have the same shape as z

• all – should I return cropped Z,X,Y or only Z?

Returns:

Z_cropped, X_cropped, Y_cropped

nmmn.lsd.delnan(x)

Remove nan elements from the array.

nmmn.lsd.delweird(x)

Remove nan or inf elements from the array.

nmmn.lsd.findnan(x)

Return index of nan elements in the array.

nmmn.lsd.nanzero(x)

Set nan elements to zero in the array.

nmmn.lsd.norm(x1, x2=None)

Normalizes x1. If also given as input x2, then normalizes x1 to x2.

Parameters:

• x1 – input array

• x2 – optional

Returns:

normalized x1

nmmn.lsd.regrid(x, y, z, xnew, ynew, method='cubic')

Regrid 1D arrays (x,y,z) – where z is some scalar field mapped at positions x,y – to a 2d array Z defined in the cartesian grids xnew,ynew (1D arrays with new grid).

For the interpolation method, choose nearest, linear or cubic.

>>> rho=regrid(d.x,d.y,d.rho,xnew,ynew)

Todo

need to create a 3d version of this method, paving the road for the 3d simulations.

nmmn.lsd.replacevals(x, minval)

Replace all values in array x for which abs(x)<=minval with x=sign(x)*minval.

nmmn.lsd.search(xref, x)

Search for the element in an array x with the value nearest xref. Piece of code based on http://stackoverflow.com/questions/2566412/find-nearest-value-in-numpy-array

>>> i=search(xref, x)

Parameters:

• xref – input number, array or list of reference values

• x – input array

Returns:

index of the x-elements with values nearest to xref:

nmmn.lsd.sortindex(x, **kwargs)

Returns the list of indexes, ordered according to the numerical value of each element of x.

Parameters:

x – input array or list.

Returns:

list of element indexes.

nmmn.lsd.string2float(s)

Converts from an array of strings to floats.

>>> string2float('28122014')

returns 28122014.0.

Parameters:

s – a string or list/array of strings

Returns:

a numpy array of floats

nmmn.lsd.uarray(x, errx)

With the new releases of the uncertainties and astropy.io.ascii (0.2.3, the replacement of asciitable), if I try to create an uncertainties array with the column of a table imported with ascii I run into trouble. For instance, if I use the sequence of commands below:

>>> import astropy.io.ascii as asciitable
>>> raff= asciitable.read('data/rafferty06.dat')
>>> m,errm=raff['mass'],raff['errm']
>>> mass=unumpy.uarray(m,errm)
>>> x=0.2*mass

I get the error message:

>>> TypeError: unsupported operand type(s) for *: 'float' and 'Column'

which I can only assume is due to the new way ascii handles tables.

I created this method to use as a replacement for unumpy.uarray that handles the tables created with astropy.io.ascii.

Usage is the same as uncertainties.unumpy.uarray.

Returns:

uncertainties array.

nmmn.misc module

Miscelaneous methods

nmmn.misc.adjustmodel(file, stretch, translate, obs)

Auxiliary method to read and normalize the BHBH simulation TS from Gold+14 to the observations.

tmod,smod=adjustmodel('/Users/nemmen/work/projects/fermi/ngc1275/Gold paper/1,2nc mdot bin.csv',5.6,2008.6,y)

obs is the data you want to normalize the model to.

Returns:

time in years, time in code units, signal

nmmn.misc.cart2pol(x, y)

Converts from cartesian to polar coordinates.

>>> r,t=cart2pol(x,y)

nmmn.misc.cart2sph(x, y)

Converts from cartesian to spherical polar coordinates, poles are at theta=0, equator at theta=90deg

>>> r,t=cart2pol(x,y)

nmmn.misc.convertyear(y)

Converts from decimal year to a python datetime tuple.

>>> convertyear(2012.9)

returns datetime.datetime(2012, 11, 24, 12, 0, 0, 3).

Parameters:

y – a float or array of floats

Returns:

a datetime structure (or list) with the date corresponding to the input float or array

Reference: http://stackoverflow.com/questions/19305991/convert-fractional-years-to-a-real-date-in-python

nmmn.misc.date2dec(date)

Convert a python datetime tuple to decimal year.

Inspired on http://stackoverflow.com/a/6451892/793218.

nmmn.misc.evalfun(fun, x, par)

Evaluates the function fun at each element of the array x, for the parameters provided in the array/list par. fun is assumed to return a scalar. Returns an array with fun evaluated at x. See example below.

Usage:

>>> p=array([1,2,3])

x=1, par0=2, par1=3

>>> fun(p)

returns a scalar

>>> x=linspace(0,10,50)

>>> evalfun(fun,x,[2,3])

evaluates fun at the array x and returns an array.

v1 Dec. 2011

nmmn.misc.findPATH(filename, envVar='PYTHONPATH')

Given a PATH or PYTHONPATH environment variable, find the full path of a file among different options. From https://stackoverflow.com/a/1124851/793218

Parameters:

• filename – file for which full path is desired

• envVar – environment variable with path to be searched

Returns:

string with full path to file

Example:

>>> fullpath=findPATH("fastregrid.cl")

nmmn.misc.lin2log(dyl, dyu, logy)

From a given uncertainty in linear space and the value of y, calculates the error in log space.

Returns a sequence with the lower and upper arrays with errors.

nmmn.misc.linefrompoints(x1, y1, x2, y2)

Given the values of two points, outputs the regression line.

Returns:

values of A,B such that y=A*x+B

nmmn.misc.log2lin(dlogyl, dlogyu, logy)

From a given uncertainty in log-space (dex) and the value of y, calculates the error in linear space.

Returns a sequence with the lower and upper arrays with errors.

nmmn.misc.mario()

Displays a nice Super Mario. :)

Analogous to mario in LaTeX.

nmmn.misc.mathcontour(x, y, errx, erry, cov)

Suppose I want to draw the error ellipses for two parameters ‘x’ and ‘y’ with 1 s.d. uncertainties and the covariance between these uncertainties. I have a mathematica notebook that does that: ‘chisq contour plot.nb’.

This method takes the values ‘x,y,errx,erry,cov’ and outputs Mathematica code that I can just copy and paste in the appropriate notebook in order to draw the ellipses.

nmmn.misc.paperimpact(citations, dt, impactfactor)

Given a journal impactfactor and a given time interval dt, this computes the expected number of citations for a given paper published in that journal over dt. It then gives the ratio of your paper’s citation over the predicted value, to give you an idea whether your paper is above or below average.

Parameters:

• citations – number of citations for your paper

• dt – time since your paper was published in years

• impactfactor – impact factor for the journal where the paper was published

nmmn.misc.pol2cart(r, th)

Converts from polar to cartesian coordinates.

>>> x,y=pol2cart(r,phi)

nmmn.misc.readmodel(file, m=100000000.0)

Auxiliary method to rescale the BHBH simulation time series from Gold+14 and compare with the data.

tphys12, t12, y12 = readmodel('Gold paper/1,2nc mdot bin.csv')

Returns:

time in years, time in code units, signal

nmmn.misc.runsave(cmd, log)

Executes command cmd and saves its standard output as log

nmmn.misc.savepartial(x, y, z, obsx, obsy, obsz, outfile)

Exports data file for partial correlation analysis with cens_tau.f. cens_tau.f quantifies the correlation between X and Y eliminating the effect of a third variable Z. I patched the Fortran code available from http://astrostatistics.psu.edu/statcodes/sc_regression.html.

Method arguments: x,y,z = arrays with data for partial correlation obs? = arrays of integers. 1 if there is a genuine measurement available and 0 if there is only an upper limit i.e. censored data.

In the case of this study, X=Pjet, Y=Lgamma, Z=distance.

The structure of the resulting datafile is:

logPjet detected? logLgamma detected? logDist detected?

where the distance is in Mpc.

Example:

>>> agngrb.exportpartial(all.kp,all.lg,log10(all.d),ones_like(all.kp),ones_like(all.kp),ones_like(all.kp),'par
tialdata.dat')

v1 Sep. 2011

nmmn.misc.scinotation(x, n=2)

Displays a number in scientific notation.

Parameters:

• x – number

• n – number of significant digits to display

nmmn.misc.sph2cart(r, th)

Converts from spherical polar to cartesian coordinates.

>>> x,y=pol2cart(r,phi)

nmmn.misc.string2year(s)

Converts from a string in the format DDMMYYYY to a python datetime tuple.

>>> string2year('28122014')

returns datetime.datetime(2014, 12, 22, 0, 0).

Parameters:

y – a string or list of strings

Returns:

a datetime structure (or list) with the date corresponding to the input float or array

Reference: https://docs.python.org/2/library/datetime.html#strftime-strptime-behavior

nmmn.misc.vel_c2p(th, vx, vy)

Computes the polar components of a velocity vector which is expressed in cartesian coordinates.

Returns: vr, vth

nmmn.misc.vel_p2c(th, vr, vth)

Computes the cartesian components of a velocity vector which is expressed in polar coordinates. i.e. apply a change of basis. See for example discussion after eq. 4 in https://ocw.mit.edu/courses/aeronautics-and-astronautics/16-07-dynamics-fall-2009/lecture-notes/MIT16_07F09_Lec05.pdf

Returns: vx, vy

nmmn.misc.whichbces(bces)

Given the ‘bces’ string selector, returns an integer which tells the location of the BCES fitting results in the arrays returned by the bces* methods.

nmmn.plots module

Fancy plots

nmmn.plots.fitconf(xdata, ydata, errx, erry, covxy, nboot=1000, bcesMethod='ort', linestyle='', conf=0.683, confcolor='gray', xplot=None, front=False, **args)

This is a wrapper that given the input data performs the BCES fit, get the orthogonal parameters and plot the best-fit line and confidence band (generated using analytical methods). I decided to put together these commands in a method because I have been using them very frequently.

Assumes you initialized the plot window before calling this method.

Usage:

>>> a1,b1,erra1,errb1,cov1=nemmen.fitconf(x[i],y[i],errx[i],erry[i],covxy[i],nboot,bces,linestyle='k',confcolor='LightGrey')

Explanation of some arguments:

• xplot: if provided, will compute the confidence band in the X-values provided

with xplot - front: if True, then will plot the confidence band in front of the data points; otherwise, will plot it behind the points

nmmn.plots.fitconfmc(xdata, ydata, errx, erry, covxy, nboot=1000, bcesMethod='ort', linestyle='', conf=1.0, confcolor='gray', xplot=None, front=False, **args)

This is a wrapper that given the input data performs the BCES fit, get the orthogonal parameters and plot the best-fit line and confidence band (generated using MC). I decided to put together these commands in a method because I have been using them very frequently.

Assumes you initialized the plot window before calling this method. This method is more stable than fitconf, which is plagued with numerical instabilities when computing the gradient.

Usage:

>>> a1,b1,erra1,errb1,cov1=nemmen.fitconf(x[i],y[i],errx[i],erry[i],covxy[i],nboot,bces,linestyle='k',confcolor='LightGrey')

Explanation of some arguments: - xplot: if provided, will compute the confidence band in the X-values provided with xplot - front: if True, then will plot the confidence band in front of the data points; otherwise, will plot it behind the points - conf: size of confidence band to be plotted in standard deviations

nmmn.plots.fitconfpred(xdata, ydata, errx, erry, covxy, nboot=1000, bces='ort', linestyle='', conf=0.68, confcolor='LightGrey', predcolor='Khaki', xplot=None, front=False, **args)

This is a wrapper that given the input data performs the BCES fit, get the orthogonal parameters and plot (i) the best-fit line, (ii) confidence band and (iii) prediction band.

I decided to put together these commands in a method because I have been using them very frequently.

Assumes you initialized the plot window before calling this method.

Usage:

>>> a1,b1,erra1,errb1,cov1=nemmen.fitconfpred(x[i],y[i],errx[i],erry[i],covxy[i],nboot,bces,linestyle='k',confcolor='LightGrey')

nmmn.plots.fitpred(xdata, ydata, errx, erry, covxy, nboot=1000, bces='ort', linestyle='', conf=0.68, predcolor='Khaki', xplot=None, front=False, **args)

This is a wrapper that given the input data performs the BCES fit, get the orthogonal parameters and plot (i) the best-fit line and (ii) prediction band.

I decided to put together these commands in a method because I have been using them very frequently.

Assumes you initialized the plot window before calling this method.

Usage:

>>> a1,b1,erra1,errb1,cov1=nemmen.fitpred(x[i],y[i],errx[i],erry[i],covxy[i],nboot,bces,linestyle='k',predcolor='LightGrey')

nmmn.plots.fourcumplot(x1, x2, x3, x4, xmin, xmax, x1leg='$x_1$', x2leg='$x_2$', x3leg='$x_3$', x4leg='$x_3$', xlabel='', ylabel="$N(x>x')$", fig=1, sharey=False, fontsize=12, bins1=50, bins2=50, bins3=50, bins4=50)

Script that plots the cumulative histograms of four variables x1, x2, x3 and x4 sharing the same X-axis. For each bin, Y is the fraction of the sample with values above X.

Arguments:

• x1,x2,x3,x4: arrays with data to be plotted

• xmin,xmax: lower and upper range of plotted values, will be used to set a consistent x-range

for both histograms. - x1leg, x2leg, x3leg, x4leg: legends for each histogram - xlabel: self-explanatory. - sharey: sharing the Y-axis among the histograms? - bins1,bins2,…: number of bins in each histogram - fig: which plot window should I use?

Inspired by Scipy.

v1 Jun. 2012: inherited from fourhists.

nmmn.plots.fourhists(x1, x2, x3, x4, xmin, xmax, x1leg='$x_1$', x2leg='$x_2$', x3leg='$x_3$', x4leg='$x_3$', xlabel='', fig=1, sharey=False, fontsize=12, bins1=10, bins2=10, bins3=10, bins4=10, line1=None, line2=None, line3=None, line4=None, line1b=None, line2b=None, line3b=None, line4b=None, loc='best')

Script that plots four histograms of quantities x1, x2, x3 and x4 sharing the same X-axis.

Arguments:

• x1,x2,x3,x4: arrays with data to be plotted

• xmin,xmax: lower and upper range of plotted values, will be used to set a consistent x-range

or both histograms. - x1leg, x2leg, x3leg, x4leg: legends for each histogram - xlabel: self-explanatory. - sharey: sharing the Y-axis among the histograms? - bins1,bins2,…: number of bins in each histogram - fig: which plot window should I use? - line?: draws vertical solid lines at the positions indicated in each panel - line?b: draws vertical dashed lines at the positions indicated in each panel

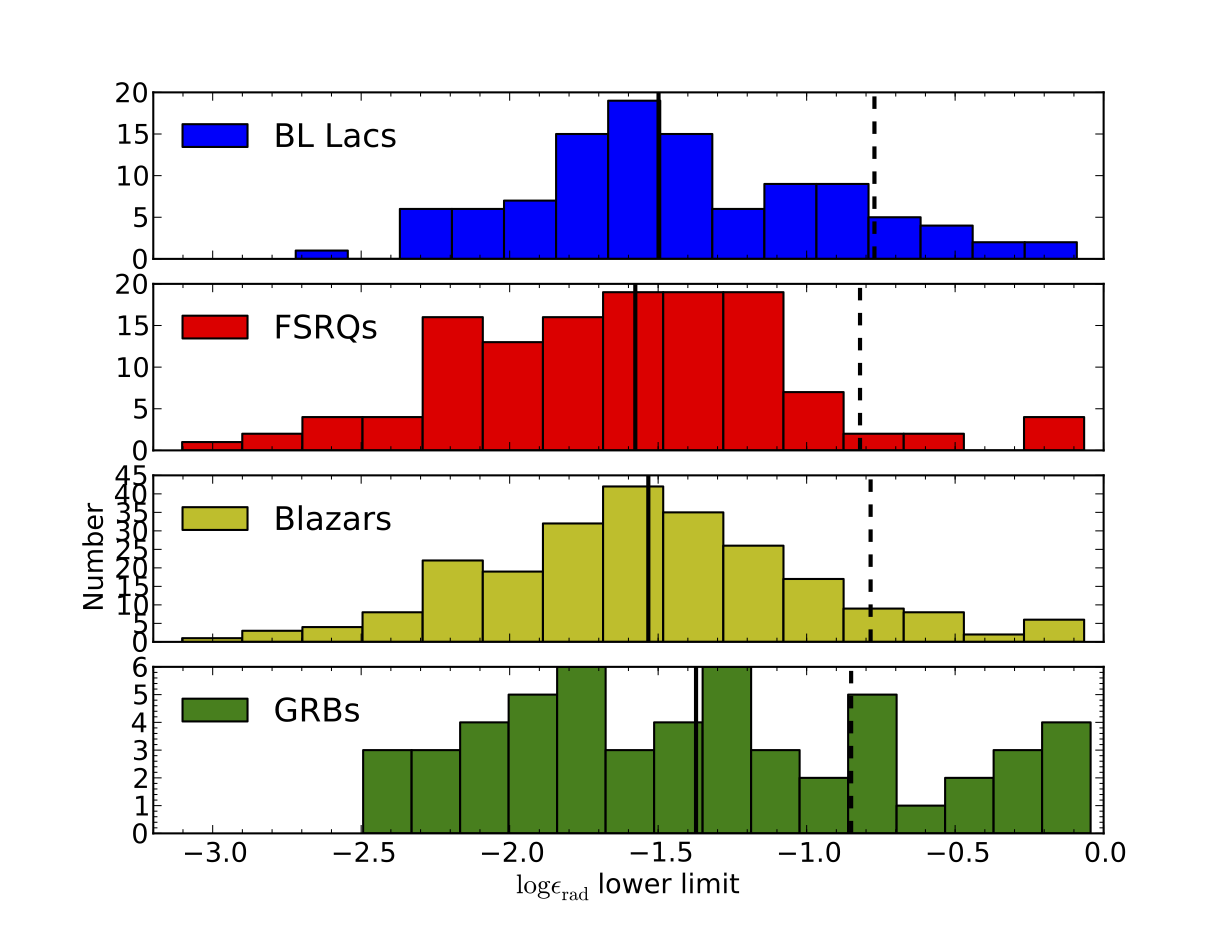
Four histograms in the same figure.

Inspired by Scipy.

nmmn.plots.image(Z, xnew, ynew, my_cmap=None, aspect='equal')

Creates pretty image. You need to specify:

nmmn.plots.ipyplots()

Makes sure we have exactly the same matplotlib settings as in the IPython terminal version. Call this from IPython notebook.

Source.

nmmn.plots.jh(xdata, ydata, errx, erry, covxy, nboot=1000, bces='ort', linestyle='', conf=0.683, confcolor='gray', xplot=None, front=False, **args)

This is a wrapper that given the input data performs the BCES fit, get the orthogonal parameters, best-fit line and confidence band. Then returns the points corresponding to the line and confidence band.

I wrote this for the John Hunter plotting contest, in order to simplify my AGN-GRB plot. Inherited from method fitconf.

Usage:

>>> x,y,lcb,ucb=nemmen.fitconf(x[i],y[i],errx[i],erry[i],covxy[i],nboot,bces,linestyle='k',confcolor='LightGrey')

where y are the line points, lcb and ucb are the lower and upper confidence band points.

Parameters:

• xplot – if provided, will compute the confidence band in the X-values provided with xplot

• front – if True, then will plot the confidence band in front of the data points; otherwise, will plot it behind the points

nmmn.plots.jointplot(X, Y, xlabel=None, ylabel=None, binsim=40, binsh=20, contour=True)

Plots the joint distribution of posteriors for X1 and X2, including the 1D histograms showing the median and standard deviations.

The work that went in creating this nice method is shown, step by step, in the ipython notebook “error contours.ipynb”. Sources of inspiration:

• http://python4mpia.github.io/intro/quick-tour.html

• http://stackoverflow.com/questions/12301071/multidimensional-confidence-intervals

Usage:

>>> jointplot(M.rtr.trace(),M.mdot.trace(),xlabel='$\log \ r_{\rm tr}$', ylabel='$\log \ \dot{m}$')

gives the following plot.

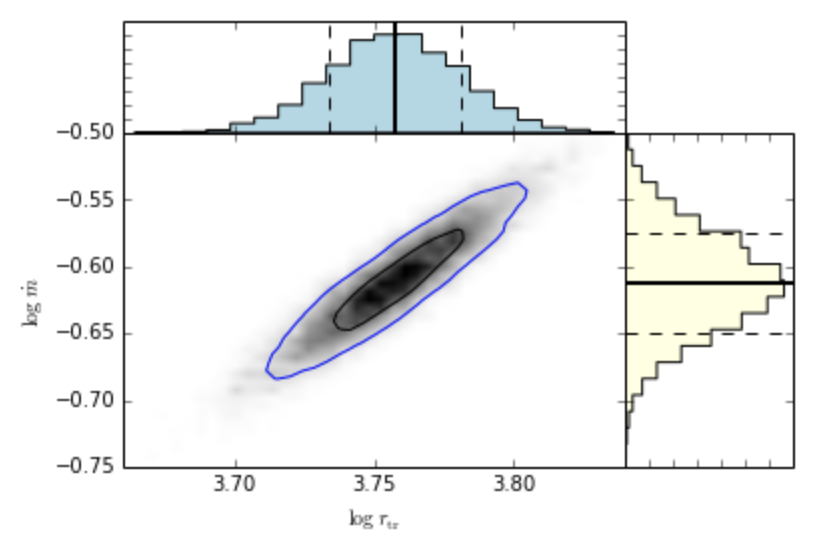
Two-dimensional kernel density distribution, along with one-dimensional histograms of each distribution.

nmmn.plots.lineWidth(value, max=1, lw_min=0.5, lw_max=10)

Ascribes a linewidth based on the input value. Useful for plots where the linewidth changes depending on some weight.

Parameters:

• value – value that will be used to get the line width

• max – maximum value for normalization

• lw_min – minimum line width

• lw_max – max line width

Returns:

line width for plotting

Example: get a sequence of stock price time series and plot them according to their relative importance in your portfolio.

>>> a=[]
>>> for i in tqdm.tqdm(range(size(acoes))): 
>>>    a.append(yf.download(tickers=acoes['col2'][i]+".SA", period=periodo, interval=dt, progress=False))
>>> for i, acao in enumerate(a): 
>>>    ar=nf.returnsTS(acao)
>>>    ar.plot(label=nome[i],lw=lineWidth(fracao[i],max(fracao)), alpha=lineWidth(fracao[i],max(fracao),0.3,1)) 

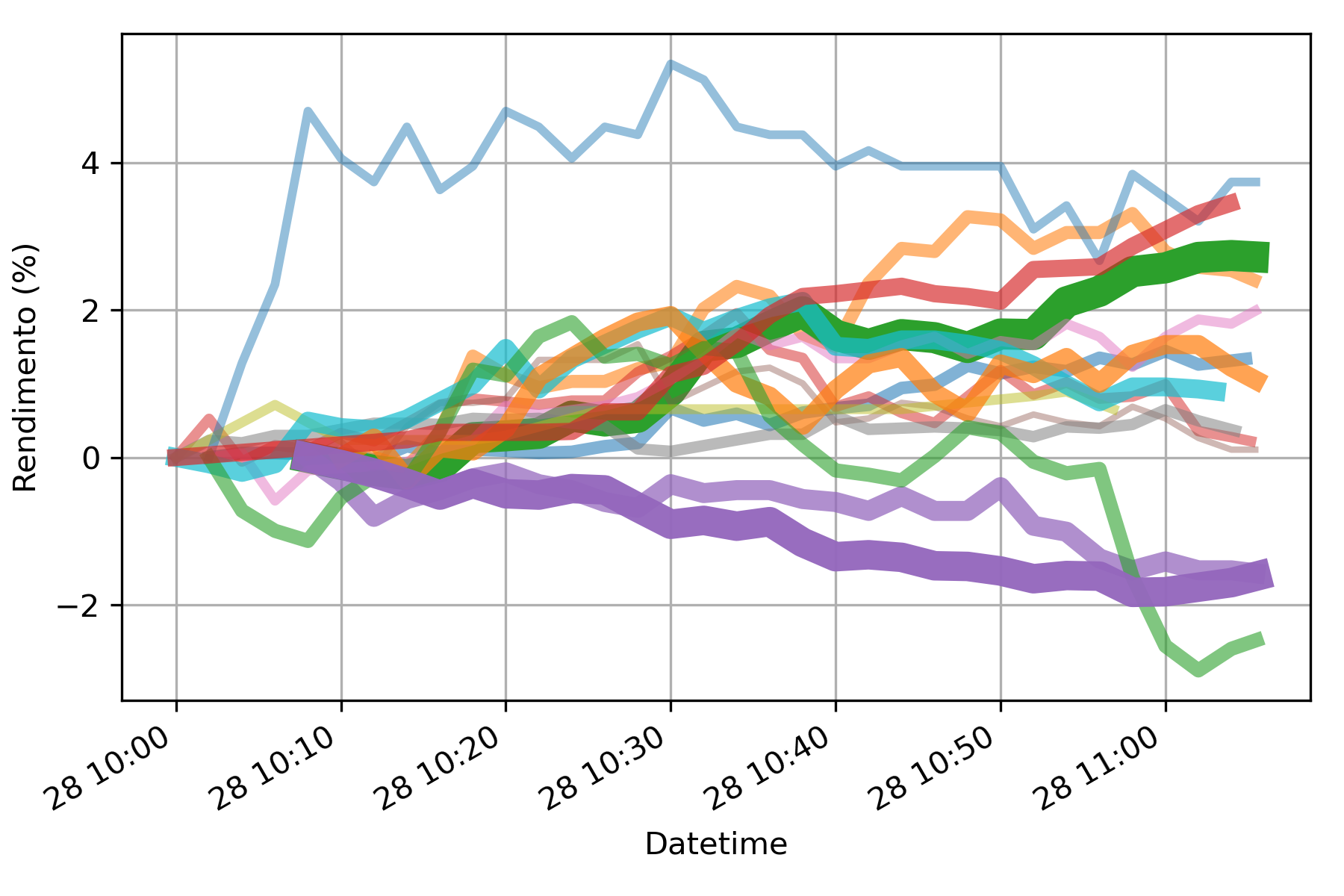
ref: https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html

nmmn.plots.make_cmap(colors, position=None, bit=False)

make_cmap takes a list of tuples which contain RGB values. The RGB values may either be in 8-bit [0 to 255] (in which bit must be set to True when called) or arithmetic [0 to 1] (default). make_cmap returns a cmap with equally spaced colors. Arrange your tuples so that the first color is the lowest value for the colorbar and the last is the highest. position contains values from 0 to 1 to dictate the location of each color.

source: http://schubert.atmos.colostate.edu/~cslocum/custom_cmap.html Chris Slocum, Colorado State University

nmmn.plots.onehist(x, xlabel='', fontsize=12)

Script that plots the histogram of x with the corresponding xlabel.

nmmn.plots.parulacmap()

Creates the beautiful Parula colormap which is Matlab’s default.

Usage:

>>> mycmap=nmmn.plots.parulacmap()
>>> imshow(rho, cmap=mycmap)

Code taken from here

nmmn.plots.plot(spec)

Returns the plot of a grmonty spectrum as a pyplot object or plot it on the screen

Parameters:

param – grmonty spectrum file

nmmn.plots.plotlinfit(xdata, ydata, a, b, erra, errb, cov, linestyle='', conf=0.683, confcolor='gray', xplot=None, front=False, **args)

This is a wrapper that given the output data from a linear regression method (for example, bayeslin.pro, the Bayesian linear regression method of Kelly (2007)), it plots the fits and the confidence bands. The input is: X, Y, slope (A), errA, intercept (B), errB and cov(A,B)

Assumes you initialized the plot window before calling this method.

Usage:

>>> nemmen.plotlinfit(x,y,a,b,erra,errb,covab,linestyle='k',confcolor='LightGrey')

Explanation of some arguments: - xplot: if provided, will compute the confidence band in the X-values provided with xplot - front: if True, then will plot the confidence band in front of the data points; otherwise, will plot it behind the points

nmmn.plots.symlog(x, C=0.43429448190325176)

Applies a modified logarithm function to x that handles negative values while maintaining continuity across zero. This function solves a very concrete problem: how to handle data that spans a huge range and has also negative values? log10 will fail. This is the answer.

The transformation is defined in an article from the journal Measurement Science and Technology (Webber, 2012):

y = sign(x)*(log10(1+abs(x)/(10^C)))

where the scaling constant C determines the resolution of the data around zero. The smallest order of magnitude shown on either side of zero will be 10^ceil(C).

Reference: MATHWORKS symlog <https://www.mathworks.com/matlabcentral/fileexchange/57902-symlog>

nmmn.plots.text(x, y, s, **args)

Version of pylab.text that can be applied to arrays.

Usage:

>>> text(x,y,s, fontsize=10)

will plot the strings in array ‘s’ at coordinates given by arrays ‘x’ and ‘y’.

nmmn.plots.threehists(x1, x2, x3, xmin, xmax, x1leg='$x_1$', x2leg='$x_2$', x3leg='$x_3$', xlabel='', fig=1, sharey=False, fontsize=12)

Script that plots three histograms of quantities x1, x2 and x3 sharing the same X-axis.

Arguments: - x1,x2,x3: arrays with data to be plotted - xmin,xmax: lower and upper range of plotted values, will be used to set a consistent x-range for both histograms. - x1leg, x2leg, x3leg: legends for each histogram - xlabel: self-explanatory. - sharey: sharing the Y-axis among the histograms? - fig: which plot window should I use?

Example: x1=Lbol(AD), x2=Lbol(JD), x3=Lbol(EHF10)

>>> threehists(x1,x2,x3,38,44,'AD','JD','EHF10','$\log L_{\rm bol}$ (erg s$^{-1}$)',sharey=True)

Inspired by Scipy.

nmmn.plots.threehistsx(x1, x2, x3, x1leg='$x_1$', x2leg='$x_2$', x3leg='$x_3$', fig=1, fontsize=12, bins1=10, bins2=10, bins3=10)

Script that pretty-plots three histograms of quantities x1, x2 and x3.

Arguments: :param x1,x2,x3: arrays with data to be plotted :param x1leg, x2leg, x3leg: legends for each histogram :param fig: which plot window should I use?

Example: x1=Lbol(AD), x2=Lbol(JD), x3=Lbol(EHF10)

>>> threehists(x1,x2,x3,38,44,'AD','JD','EHF10','$\log L_{\rm bol}$ (erg s$^{-1}$)')

Inspired by http://www.scipy.org/Cookbook/Matplotlib/Multiple_Subplots_with_One_Axis_Label.

nmmn.plots.turbocmap()

Returns the Turbo colormap: an improved version of the awful jet colormap.

The look-up table contains 256 entries. Each entry is a floating point sRGB triplet.

Usage:

>>> turbo=nmmn.plots.turbocmap()
>>> imshow(rho, cmap=turbo)

Copyright 2019 Google LLC. SPDX-License-Identifier: Apache-2.0 Author: Anton Mikhailov

References:

• turbo colormap array

• Google AI blog post describing the advantages of the colormap

nmmn.plots.twohists(x1, x2, xmin, xmax, range=None, x1leg='$x_1$', x2leg='$x_2$', xlabel='', fig=1, sharey=False, fontsize=12, bins1=10, bins2=10)

Script that plots two histograms of quantities x1 and x2 sharing the same X-axis.

Parameters:

• x1,x2 – arrays with data to be plotted

• xmin,xmax – lower and upper range of plotted values, will be used to set a consistent x-range for both histograms.

• x2leg (x1leg,) – legends for each histogram

• xlabel – self-explanatory.

• bins1,bins2 – number of bins in each histogram

• fig – which plot window should I use?

• range – in the form (xmin,xmax), same as range argument for hist and applied to both histograms.

Inspired by Scipy.

nmmn.plots.uerrorbar(ux, uy, **args)

Adaptation of pylab.errorbar to work with arrays defined using the uncertainties package, which include the errorbars built-in.

Usage:

>>> uerrorbar(x,y,fmt='o')

will plot the points and error bars associated with the ‘unumpy’ arrays x and y

nmmn.plots.wolframcmap()

Returns colormap that matches closely the one used by default for images in Wolfram Mathematica 11 (dark blue to orange).

I spent one hour playing around to reproduce it.

Usage:

>>> mycmap=nmmn.plots.wolframcmap()
>>> imshow(rho, cmap=mycmap)

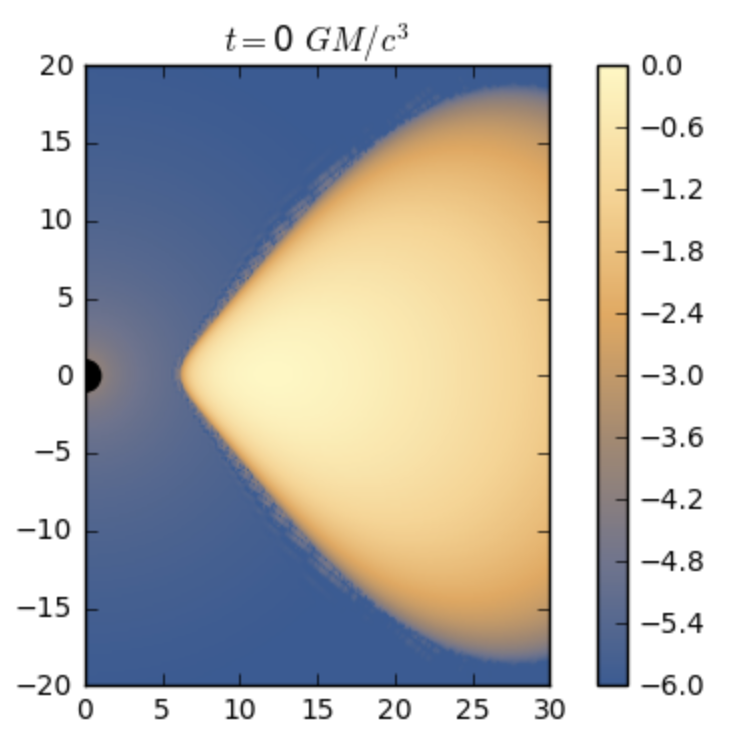
Image plotted using Wolfram’s colormap.

nmmn.sed module

Spectral energy distributions

Methods and classes for dealing with spectral energy distributions (SEDs).

class nmmn.sed.SED(file=None, logfmt=0, lognu=None, ll=None)

Bases: object

Class that defines objects storing Spectral energy distributions (SEDs). The SEDs can be imported either from datafiles with the observations/models, or from arrays with the values of log(nu) and log(nuLnu).

The object’s initial attributes are:

• nu: frequency in Hertz

• lognu: log10(frequency)

• nlnu: nu L_nu in erg/s

• ll: log10(nu Lnu)

• file : input datafile

To import a SED from an ASCII file:

>>> s=sed.SED(file=datafile, logfmt=XX)

where logfmt is 1 if the data is already in logarithm or 0 otherwise. NOTE: logfmt for now is by default 0 (Eracleous’ SEDs).

To create a SED object from the arrays lognu and lognulnu:

>>> s=sed.SED(lognu=lognu, ll=lognulnu)

To import a SED in a special format:

>>> s=sed.SED()
>>> s.erac('ngc1097.dat')

To plot the SED:

>>> plot(s.lognu, s.ll)

To calculate the bolometric luminosity:

>>> s.bol()

after which the value will be stored in s.lumbol

alphaox()

Computes the alpha_ox index.

>>> alphaox=s.alphaox()

bol(lognu0=None, lognu1=None, xrange=[8, 22])

Calculates the bolometric luminosity of the SED. Performs the integration using the trapezoidal rule. Adds the attribute lumbol to the object with the result.

>>> s.bol()

makes the variable s.lumbol hold the bolometric luminosity.

>>> s.bol(17, 20)

makes s.lumbol hold the luminosity integrated in the range 1e17-1e20 Hz.

>>> s.bol(18, 20, [s.lognu[0],s.lognu[-1]])

gives the integrated luminosity in the range 1e18-1e20 Hz. Before integrating, interpolates the SED over its original frequency range with 1000 points.

check()

Checks whether there are NaN or Inf values in the array log10(nuLnu). If so, displays a warning to the user and the corresponding filename. Method called by initialization methods init and erac.

Creates a new attribute, weird, which is 1 if there are NaN or Inf values, and 0 otherwise.

chisq(model, npars=None)

Computes the goodness of fit between the observed SED (assumed to be “self”) and the given model. If you don’t provide the number of free parameters in the model, it returns a modified chi squared (modified in the sense that it assumes the uncertainties in all data points to be unity). If you provide npars it returns the modified reduced chi squared.

>>> s.chisq(m)
returns the (modified) chi square with s and m being the observed and model
SEDs, respectively.

>>> s.chisq(m,4)
returns the reduced chi square.

NOTE: this method was written assuming that the observed SEDs correspond to Eracleous’ SEDs. Needs to be adapted in order to be applied to other types of SEDs. We discard the 100 keV interpolation done by EHF10.

copy()

Returns a copy of the current SED object. Use this in the same way you would use the numpy copy() method to avoid changing the attributes of a SED unintentionally.

edd(mass=None)

Computes the Eddington ratio \(L_{\rm bol}/L_{\rm} Edd}\). First computes the bolometric luminosity via interpolation and then calculates the Eddington ratio.

Parameters:

mass – log10(BH mass in solar masses)

erac(file)

Reads SEDs in the format provided by Eracleous et al. LINER SEDs: nu nuLnu nuLnu(extinction) error upperLimit?(0/1)

Adds the following attributes to the SED object: - nlnuex: nuLnu after extinction correction - llex: log10(nuLnu) after extinction correction - ul: is the datapoint an upper limit (arrow)? 1 if yes, 0 if not

findlum(x)

Given the input frequency in units of log(nu/Hz), returns the list [log(nu), Lnu] with the frequency and luminosity closest to the specified value.

>>> lognu,lum=s.findlum(14)

will look for the freq. and lum. nearest nu=10^14 Hz

geomean(seds, nuref=17.684, refnlnu=1e+40, xray=None)

Given a list of SEDs and a reference value of log10(nu), normalizes the SEDs (s.normalize) at the given nuref and refnlnu, calculates the geometric mean of their luminosities (average(log10(nuLnu)), like Eracleous et al. 2010 does) and returns the list [mean,sd] where ‘mean’ is SED object with the geometric mean and ‘sd’ is the object with the standard deviation.

Alternatively, if the user provides the argument xray=True, then the method normalizes the SEDs such that they have the same X-ray luminosity refnlnu in the range 2-10 keV (thus ignoring the arg. nuref).

>>> means=s.mean([s1,s2],17.684,1e40)

returns mean <- [lognu, <s1,s2>], where <s,s1,s2> -> <log10[nuLnu(s),nuLnu(s1),nuLnu(s2)]>, lognu being the common units of frequency for the SEDs after interpolation.

>>> means=s.mean([s1,s2],refnlnu=1e40,xray=True)

returns the mean after normalizing the SEDs to the X-ray lum. 1e40 erg/s in the range 2-10 keV.

grmonty(file)

Reads SEDs in the format provided by grmonty. I ported the original SM script plspec.m provided by J. Dolence.

hayden(file, dist)

Reads SEDs in the format provided by Hampadarath et al.:

nu(GHz) flux(microJy) error(microJy) Detection[1]orUpperlimit[0]

Adds the following attributes to the SED object: - ul: is the datapoint an upper limit (arrow)? 1 if yes, 0 if not - distance: distance to object in Mpc

haydenx(file)

Reads X-ray data in the format provided by F. Panessa: nu error_nu nuLnu error ?

Adds the following attributes to the SED object: - ul: is the datapoint an upper limit (arrow)? 1 if yes, 0 if not

interp(seds=None, points=1000, xrange=[8, 22])

Interpolates the SED and a list of SEDs (optional) in the given range of values of log(nu) and for the given number of points.

>>> s.interp([s,s1,s2])
interpolates s, s1 and s2 with 1000 points in the range
log(nu)=8-22 (Hz). s, s1 and s2 are also instances of the class SED. The
interpolated arrays (lognui, lli, nui, nlnui) will be added as new 
attributes to each object. If given no argument, will interpolate the
current SED object.

Parameters:

• seds – list of SED objects to interpolate

• points – number of interpolated points

• xrange – list in the form [xinitial, xfinal] with the x-range of interpolation.

If provided with no list of SEDs (e.g., s.interp()), then the method interpolates only the current SED s. If provided with no xrange argument, it will by default assume the range [8,22] discarding data points outside that range in the interpolation, hence adjust accordingly.

ion()

Calculates the rate of ionizing photons in the SED.

>>> q=s.ion()

mean(seds, nuref=17.684, refnlnu=1e+40, xray=None)

Given a list of SEDs and a reference value of log10(nu), normalizes the SEDs (s.normalize) at the given nuref and refnlnu, calculates the average of their luminosities (average(log10(nuLnu)), like Eracleous et al. 2010 does) and returns the list [mean,sd] where ‘mean’ is SED object with the mean and ‘sd’ is the object with the standard deviation.

Alternatively, if the user provides the argument xray=True, then the method normalizes the SEDs such that they have the same X-ray luminosity refnlnu in the range 2-10 keV (thus ignoring the arg. nuref).

>>> means=s.mean([s1,s2],17.684,1e40)

returns mean <- [lognu, <s1,s2>], where <s,s1,s2> -> <log10[nuLnu(s),nuLnu(s1),nuLnu(s2)]>, lognu being the common units of frequency for the SEDs after interpolation.

>>> means=s.mean([s1,s2],refnlnu=1e40,xray=True)

returns the mean after normalizing the SEDs to the X-ray lum. 1e40 erg/s in the range 2-10 keV.

meanlin(seds, nuref=17.684, refnlnu=1e+40)

Given a list of SEDs and a reference value of log10(nu), normalizes the SEDs (s.normalize) at the given nuref and refnlnu, calculates the average of their luminosities (log10(average nuLnu)) and returns the list [mean,sd] where ‘mean’ is SED object with the mean and ‘sd’ is the object with the standard deviation.

>>> mean=s.meanlin([s1,s2],17.684,1e40)
returns mean <- [lognu, <s1,s2>],
where <s,s1,s2> -> log10[<nuLnu(s),nuLnu(s1),nuLnu(s2)>], lognu being the common 
units of frequency for the SEDs after interpolation.

median(seds, nuref=17.684, refnlnu=1e+40, xray=None)

Given a list of SEDs and a reference value of log10(nu), normalizes the SEDs (s.normalize) at the given nuref and refnlnu, calculates the average of their luminosities (average(log10(nuLnu)), like Eracleous et al. 2010 does) and returns the list [mean,sd] where ‘mean’ is SED object with the median and ‘sd’ is the object with the standard deviation.

Alternatively, if the user provides the argument xray=True, then the method normalizes the SEDs such that they have the same X-ray luminosity refnlnu in the range 2-10 keV (thus ignoring the arg. nuref).

>>> means=s.median([s1,s2],17.684,1e40)

returns median <- [lognu, <s1,s2>], where <s,s1,s2> -> <log10[nuLnu(s),nuLnu(s1),nuLnu(s2)]>, lognu being the common units of frequency for the SEDs after interpolation.

>>> means=s.median([s1,s2],refnlnu=1e40,xray=True)

returns the mean after normalizing the SEDs to the X-ray lum. 1e40 erg/s in the range 2-10 keV.

normalize(seds=None, nuref=17.684, refnlnu=1e+40, xray=None)

Normalizes a SED at the given frequency (lognu/Hz) and nuLnu (erg/s). NOTE: this will modify the SED(s). Alternatively, if the user provides the argument xray=True, then the method normalizes the SEDs such that they have the same X-ray luminosity refnlnu in the range 2-10 keV (thus ignoring the arg. nuref).

>>> s.normalize([s1,s2,s3])

normalizes the SEDs in the object list at the same frequency and nuLnu

>>> s.normalize([s1,s2,s3],refnlnu=1e40,xray=True)

normalizes the SEDs such that they have the same X-ray luminosity 1e40 erg/s in the range 2-10 keV.

The method is designed to automatically call the interp method (e.g., s.interp([s1,s2])) if needed.

prieto(file, dist)

Reads SEDs in the format provided by Hampadarath et al.:

nu(Hz) nu*F_nu(Jy Hz)

Adds the following attributes to the SED object: - distance: distance to object in Mpc

radioloud()

Computes the radio-loudness for the SED. Adds the attribute rl to the object with the result. If Ro>=10. we have a RL AGN, otherwise it is a RQ one.

>>> rl=s.radioloud()

makes the variable s.rl hold the radio-loudness.

raniere(file, dist)

Reads SEDs in the format provided by Hampadarath et al.: nu(GHz) flux(microJy) error(microJy) Detection[1]orUpperlimit[0]

Parameters:

• file – file with SED data

• dist – distance in Mpc

Returns:

SED object in units of Hz vs erg/s

Adds the following attributes to the SED object: - ul: is the datapoint an upper limit (arrow)? 1 if yes, 0 if not - distance: distance to object in Mpc

sort()

>>> s.sort()

Sorts the SED in ascending order of frequencies.

unit()

Normalizes the spectrum to one.

write(file)

Exports the SED as an ASCII file with the structure: col1=log10(nu/Hz), col2=log10(nu Lnu / erg per sec)

>>> s.write(file)

exports the SED s as the file “file”

xrays()

Calculates the photon index of the X-ray spectrum and Lx (2-10 keV). Stores the new attributes gammax and lumx in the object.

>>> Lx,gamma=s.xrays()

creates the new attributes s.lumx and s.gammax

nmmn.sed.f(xpop, ypop, x)

Given the spectrum of a popstar and an array of frequencies ‘x’, this outputs the values of ypop for each x.

Parameters:

• x – frequencies

• xpop,ypop – spectrum from stellar population

Returns:

returns y=a*L where L is the stellar pop. luminosity

nmmn.sed.groupmodel(sum=None, ssd=None, jet=None, adaf=None)

Groups the different components of a SED model into one dictionary for convenient access. The model component SEDs are assumed to have been imported using the SED class. This method is used in the plot method.

Example:

Imports the model SEDs: >>> s=SED(file=’sum.dat’, logfmt=1) >>> disk=SED(file=’disk.dat’, logfmt=1) >>> a=SED(file=’adaf.dat’, logfmt=1)

Groups them together in a dictionary d: >>> d=groupmodel(sum=s,ssd=disk,adaf=a) returning {‘sum’:s,’ssd’:disk,’adaf’:a}.

nmmn.sed.haydenobs(source, patho='/Users/nemmen/work/projects/hayden/all/', info='/Users/nemmen/work/projects/hayden/info.dat')

Plots the observed SED from the Hayden et al. sample. Includes arrows for upper limits and the nice bow tie.

Extinction corrections represented as either “error bars” or “circle + error bar”.

Parameters:

• source – source name e.g. ‘NGC1097’ or ‘ngc1097’ or ‘NGC 1097’. Must have four numbers.

• patho – path to observed SED data files

• info – path to information datafile with distances and masses

Returns:

SED object

nmmn.sed.haydensed(source, patho='/Users/nemmen/work/projects/hayden/all/', info='/Users/nemmen/work/projects/hayden/info.dat')

Reads an observed SED from the Hayden et al. sample. Computes useful quantities.

Parameters:

• source – source name e.g. ‘NGC1097’ or ‘ngc1097’ or ‘NGC 1097’. Must have four numbers.

• patho – path to observed SED data files

• info – path to information datafile with distances and masses

Returns:

SED object

nmmn.sed.modelplot(ssdf, adaff, jetf, sumf, **args)

Plots the model components.

Arguments: The filenames of each model component.

nmmn.sed.modelsplot(pathm='/Users/nemmen/Dropbox/work/projects/adafjet/', jetfile=None, showthin=True, showjet=True, showsum=True, showadaf=[True, True, True])

Nice wrapper that plots 3 models computed with the ADAF Fortran code available at ~/work/projects/adafjet/adaf.

Useful when modeling a given SED.

Input:

• *file : path to ASCII files containing the precomputed models

• showadafshould I display the three ADAF models? (list or array of booleans,

  e.g., [True,True,True])

• showthin : Include thin disk?

• showjet : Display jet?

• showsum : Show sum of components?

nmmn.sed.obsplot(source, table='/Users/nemmen/Dropbox/work/projects/finished/liners/tables/models.csv', patho='/Users/nemmen/Dropbox/work/projects/finished/liners/seds/obsdata/', ext='0')

Plots the observed SED taken from the Eracleous et al. sample. Includes arrows for upper limits and the nice bow tie.

Extinction corrections represented as either “error bars” or “circle + error bar”.

Parameters:

• source – source name e.g. ‘NGC1097’ or ‘ngc1097’ or ‘NGC 1097’. Must have four numbers.

• table – path of ASCII table models.csv with the required SED parameters gammax, error in gammax, X-ray luminosity and distratio

• patho – path to observed SED data files

• ext – 0 for showing extinction corrections as “error bars”; 1 for “circle + error bar”

Returns:

SED object with distance-corrected luminosities

nmmn.sed.obsplot1097(source, o, table)

Modification of the plot method to handle the nice data of NGC 1097.

Parameters:

• source – source name e.g. ‘NGC1097’ or ‘ngc1097’ or ‘NGC 1097’. Must have four numbers.

• o – observed SED data points imported using the SED class and the erac method.

• table – path of ASCII table models.csv with the required SED parameters gammax, error in gammax, X-ray luminosity and distratio.

Returns:

SED object with distance-corrected luminosities

nmmn.sed.pionDecay(logfile, parfile, alpha=2.3, E0=None, proton_energy=None, photon_energy=None)

Computes the gamma-ray spectrum from pp collisions followed by pion decay for the full RIAF computed by my semi-analytical model.

Parameters:

• logfile – log file generated by the semi-analytical RIAF model, containing the electron number density and ion temperature. e.g. ‘cd ~/science/projects/adafjet/adaf/perl/run01/out_01’

• parfile – parameter file used as input by the semi-analytical RIAF model, containing the black hole mass and other model parameters. e.g. ‘cd ~/science/projects/adafjet/adaf/perl/run01/in.dat’

• alpha – power-law index

• E0 – reference energy. Default = proton_mass*c^2 ~ 1 GeV

• proton_energy – array of proton energies, e.g. logspace(0, 6, 50) * astropy.units.MeV

• photon_energy – array of photon energies for SED. If None, taken as the same as proton_energy. In astropy.units

Returns:

SED object in units of Hz vs erg/s

Example:

Computes gamma-ray SED with default particle DF options and power-law index. Issue the command below in the directory with model datafiles.

m=nmmn.sed.pionDecay('out_01','in.dat')
plot(m.lognu,m.ll)

Based on the jupyter notebook “gamma-rays RIAF”.

References about pion decay physics: • Oka & Manmoto 2003: overview of calculation • Fatuzzo & Melia 2003: overview of calculation • Dermer 1986: formulas

naima model: • Kafexhiu, E., Aharonian, F., Taylor, A.M., & Vila, G.S. 2014, Physical Review D, 90, 123014 • Zabalza 2015

nmmn.sed.plot(source, o, m, table)

DEPRECATED. Split these method in separate units: modelplot, obsplot, plotprops. Main method to create the SED plot.

Arguments: - source: source name e.g. ‘NGC1097’ or ‘ngc1097’ or ‘NGC 1097’. Must have four

numbers.

• o: observed SED data points imported using the SED class and the erac method.

• m: dictionary with the different model components created with the method

  groupmodel below.

• table: path of ASCII table models.csv with the required SED parameters gammax,

  error in gammax, X-ray luminosity and distratio.

nmmn.sed.plotprops(labelfontsize=18, legend=True, option=1, loc='upper right')

Define other properties of the SED plot: additional axis, font size etc.

nmmn.sed.popstar(o)

Fits the stellar population spectrum, finds the required mass and plots its SED.

Parameters:

o – object containing the observed SED

Returns:

fitted stellar population mass

nmmn.sed.powerlaw(alpha, Lx, nurange, npoints=10)

Calculates the X-ray powerlaw variables.

Arguments: - alpha: spectral power-law index - Lx: total luminosity in X-rays in the nurange

• nurange: two-element list or array with range of frequencies to plot,

in keV. e.g. [2,10]

Returns the sequence of arrays log10(nu),log10(nu*Lnu) for plotting.

nmmn.sed.sum(seds)

Given a list of SEDs previously interpolated in the same binning, sums their luminosities and returns a SED object with the sum.

>>> ss=sum([s,s1,s2])

returns the SED ss <- [lognu, s+s1+s2], where s+s1+s2 -> log10[nuLnu(s)+nuLnu(s1)+nuLnu(s2)], lognu being the common units of frequency for the SEDs after interpolation.

The method is designed to automatically call the interp method for each SED if needed.

nmmn.sed.xray(L2_10, gammax, gammaerru, gammaerrl, nurange=[2.0, 10.0], **args)

Plots X-ray “bow tie”, provided the X-ray luminosity in the 2-10 keV range, the best-fit photon index and the error in this index.

Arguments: - L2_10: X-ray luminosity in the 2-10 keV range, erg/s - gammax: best-fit photon index - gammaerru, gammaerrl: upper and lower 1sigma error bars on the value of

gammax

• nurange: two-element list or array with range of frequencies to plot,

in keV. e.g. [2,10]

nmmn.sed.xrayinset(source, ssdf, adaff, jetf, sumf, table='/Users/nemmen/Dropbox/work/projects/finished/liners/tables/models.csv', **args)

Plots an inset with the zoomed-in X-ray spectra.

nmmn.stats module

Statistical methods

• fit residuals

• Computing prediction and confidence bands

• Comparing goodness-of-fit of different models

• operations on statistical distributions

• custom statistical distributions

• p-values and significance

nmmn.stats.aic(k, n, rss, errors=False)

Computes the Akaike information criterion which is “a measure of the relative goodness of fit of a statistical model”. Unlike the F-test, it does not assume that one model is a particular case of the more complex one. If errors==False then assume the errors are the same for every data point. Otherwise, assumes you are providing the chi-squared values instead of RSS.

Usage:

>>> aic = aic(k,n,rss)

Parameters:

• rss – residual sum of squares for the model in case errors=False, otherwise assumes you are giving the chi-square values

• n – sample size, i.e. number of data points

• k – number of free parameters in the model

Returns:

AIC statistic

References:

1. Documentation for Origin software on fit comparison: http://www.originlab.com/index.aspx?go=Products/Origin/DataAnalysis/CurveFitting/NonlinearFitting&pid=1195 (first heard about this test there)

2. http://en.wikipedia.org/wiki/Akaike_information_criterion

v1 Dec 2011

nmmn.stats.bic(k, n, rss, errors=False)

Computes the Bayesian information criterion which is “a criterion for model selection among a finite set of models”. From wikipedia: “The BIC […] introduces a penalty term for the number of parameters in the model. The penalty term is larger in BIC than in AIC.”

In order to use BIC to quantify the evidence against a specific model, check out the section “use of BIC” in the presentation “171:290 Model Selection, Lecture VI: The Bayesian Information Criterion” by Joseph Cavanaugh (http://myweb.uiowa.edu/cavaaugh/ms_lec_6_ho.pdf).

If errors==False then assume the errors are the same for every data point. Otherwise, assumes you are providing the chi-squared values instead of RSS.

Usage: >>> bic = bic(k,n,rss)

Arguments: - rss : residual sum of squares for the model in case errors=False, otherwise assumes you are giving the chi-square values - n : sample size, i.e. number of data points - k : number of free parameters in the model

Returns: BIC statistic

References: 1. http://en.wikipedia.org/wiki/Bayesian_information_criterion 2. Model Selection, Lecture VI: The Bayesian Information Criterion” by Joseph Cavanaugh (http://myweb.uiowa.edu/cavaaugh/ms_lec_6_ho.pdf)

v1 Apr 2012

nmmn.stats.bootcorr(x, y, nboot)

Given (X,Y) data points with intrinsic scatter, computes the bootstrapped Pearson and Spearman correlation coefficients. This will give you an idea of how much outliers affect your correlation.

Usage:

>>> r,rho=bootcorr(x,y,100000)

performs 100000 bootstrapping realizations on the arrays x and y.

Returns:

r - array with bootstrapped Pearson statistics

Returns:

rho - bootstrapped array with Spearman statistics

nmmn.stats.chisq(x, y, a=None, b=None, sd=None)

Returns the chi-square error statistic as the sum of squared errors between Y(i) and AX(i) + B. If individual standard deviations (array sd) are supplied, then the chi-square error statistic is computed as the sum of squared errors divided by the standard deviations. Inspired on the IDL procedure linfit.pro. See http://en.wikipedia.org/wiki/Goodness_of_fit for reference.

If a linear model is not provided via A,B (y=ax+b) then the method computes the chi-square using the best-fit line.

x,y,sd assumed to be Numpy arrays. a,b scalars. Returns the float chisq with the chi-square statistic.

nmmn.stats.chisqg(ydata, ymod, sd=None)

Returns the chi-square error statistic as the sum of squared errors between Ydata(i) and Ymodel(i). If individual standard deviations (array sd) are supplied, then the chi-square error statistic is computed as the sum of squared errors divided by the standard deviations. Inspired on the IDL procedure linfit.pro. See http://en.wikipedia.org/wiki/Goodness_of_fit for reference.

x,y,sd assumed to be Numpy arrays. a,b scalars. Returns the float chisq with the chi-square statistic.

nmmn.stats.chisqxy(x, y, errx, erry, a, b)

Returns the chi-square error statistic for a linear fit, computed taking into account the errors in both X and Y (i.e. the effective variance). See equation 3 in Ascenso et al. 2012, A&A or Yee & Ellingson 2003 ApJ.

Usage:

>>> chisq=chisqxy(xdata,ydata,errx,erry,a,b)

where

• xdata,ydata : data

• errx,erry : measurement uncertainties in the data

• a,b : slope and intercept of the best-fit linear regression model

nmmn.stats.conf2sig(p)

Given a confidence p-value, translates it into standard deviations. E.g., p=0.683 -> 1sigma, p=0.954 -> 2sigma, etc.

Inspired on p2sig method.

Usage:

>>> s=conf2sig(0.683)

nmmn.stats.confband(xd, yd, a, b, conf=0.95, x=None)

Calculates the confidence band of the linear regression model at the desired confidence level, using analytical methods. The 2sigma confidence interval is 95% sure to contain the best-fit regression line. This is not the same as saying it will contain 95% of the data points.

Arguments:

• conf: desired confidence level, by default 0.95 (2 sigma)

• xd,yd: data arrays

• a,b: linear fit parameters as in y=ax+b

• x: (optional) array with x values to calculate the confidence band. If none is provided, will by default generate 100 points in the original x-range of the data.

Returns: Sequence (lcb,ucb,x) with the arrays holding the lower and upper confidence bands corresponding to the [input] x array.

Usage:

>>> lcb,ucb,x=nemmen.confband(all.kp,all.lg,a,b,conf=0.95)
calculates the confidence bands for the given input arrays

>>> pylab.fill_between(x, lcb, ucb, alpha=0.3, facecolor='gray')
plots a shaded area containing the confidence band

References: 1. http://en.wikipedia.org/wiki/Simple_linear_regression, see Section Confidence intervals 2. http://www.weibull.com/DOEWeb/confidence_intervals_in_simple_linear_regression.htm

v1 Dec. 2011 v2 Jun. 2012: corrected bug in computing dy

nmmn.stats.confbandmc(x, par, varcov, n=100000, sigmas=1.0)

Calculates the 1sigma confidence band of a linear model without needing to specify the data points, by doing a Monte Carlo simulation using the Multivariate normal distribution. Assumes the parameters follow a 2D normal distribution.

Arguments:

• x: array with x values to calculate the confidence band.

• par : array or list with structure [par0, par1, par2, …] with the best-fit parameters

• varcov : variance-covariance matrix of the parameters

• n : number of (a,b) points generated from the multivariate gaussian

• sigmas : number of standard deviations contained within the prediction band

Output:

• lcb, ucb : lower and upper prediction bands

• y : values of the model tabulated at x

Usage:

>>> lcb,ucb,y=nemmen.confbandmc(x,bfit,bcov)
calculates the prediction bands for the given input arrays

>>> pylab.fill_between(x, lcb, ucb, alpha=0.3, facecolor='gray')
plots a shaded area containing the prediction band

nmmn.stats.confbandnl(xd, yd, fun, par, varcov, deg, conf=0.95, x=None)

Calculates the confidence band of a nonlinear model at the desired confidence level, using analytical methods.

Arguments:

• xd,yd: data arrays

• fun : function f(v) - the model - which returns a scalar. v is an array such that v[0]=x (scalar), v[i>0] = parameters of the model

• par : array or list with structure [par0, par1, par2, …] with the best-fit parameters that will be fed into fun

• varcov : variance-covariance matrix obtained from the nonlinear fit

• deg : number of free parameters in the model

• conf: desired confidence level, by default 0.95 (2 sigma)

• x: (optional) array with x values to calculate the confidence band. If none is provided, will by default generate 100 points in the original x-range of the data.

Usage:

>>> lcb,ucb,x=nemmen.confbandnl(all.kp,all.lg,broken,bfit,bcov,4,conf=0.95)
calculates the confidence bands for the given input arrays

>>> pylab.fill_between(x, lcb, ucb, alpha=0.3, facecolor='gray')
plots a shaded area containing the prediction band  

Returns:

Sequence (lcb,ucb,x) with the arrays holding the lower and upper confidence bands

corresponding to the [input] x array.

References:

1. How does Prism compute confidence and prediction bands for nonlinear regression?

2. http://stats.stackexchange.com/questions/15423/how-to-compute-prediction-bands-for-non-linear-regression

3. see also my notebook

nmmn.stats.credbandmc(x, slope, inter, sigmas=1.0)

Calculates the confidence (or credibility in case of Bayesian analysis) band of a linear regression model, given the posterior probability distributions of the slope and intercept (presumably computed via Bayesian regression, see bayeslin.pro). These distributions do not need to be normal.

Arguments:

• x: array with x values to calculate the confidence band.

• slope, inter: posterior distributions of slope and intercept for linear regression

• sigmas : number of standard deviations contained within the confidence band

Output:

• lcb, ucb : lower and upper confidence bands

• y : best-fit values of the model tabulated at x

Usage:

>>> lcb,ucb,y=nemmen.predbandmc(x,a,b)
calculates the prediction bands for the given input arrays

>>> pylab.fill_between(x, lcb, ucb, alpha=0.3, facecolor='gray')
plots a shaded area containing the prediction band

v1 Jun. 2012: inspired by private communication with B. Kelly.

nmmn.stats.fitstats(xdata, ydata, errx, erry, a, b)

Computes different useful statistics for the given (X +- errX, Y +- errY) arrays of data. Also quantifies the goodness-of-fit of the provided linear fit with slope ‘a’ and intercept ‘b’.

Usage:

>>> r,rho,rchisq,scat,iscat,r2=fitstats(xdata,ydata,errx,erry,a,b)

param xdata,ydata:

data

param errx,erry:

measurement uncertainties in the data

param a,b:

slope and intercept of the best-fit linear regression model

Returns:

• Pearson ‘r’

• Spearman ‘rho’

• Reduced chi-squared ‘chi^2_nu’

• raw scatter about the best-fit

• intrinsic scatter

• Coefficient of determination ‘R^2’

nmmn.stats.ftest(rss1, rss2, n, p1, p2)

Carries out the F-test to decide which model fits the data better. Computes the F statistic, associated p-value and the significance in sigmas with which we can reject the null hypothesis. You can also give the \(\chi^2\) values instead of RSS if you have y-errors.

Note that p2>p1 must be obeyed, i.e. model 2 is “nested” within model 1.

Usage:

>>> fstat,pvalue,conf = ftest(rss1,rss2,n,p1,p2)

Arguments: - rss1, rss2 : residual sum of squares for models 1 and 2 - n : sample size, i.e. number of data points - p1, p2 : number of free parameters in the models

Returns: - fstat : the F statistic - pvalue : p-value associated with the F statistic - conf : significance in sigmas with which we can reject the null hypothesis

References: 1. http://en.wikipedia.org/wiki/F-test 2. http://graphpad.com/curvefit/2_models__1_dataset.htm, Graphpad.com, Comparing the fits of two models (CurveFit.com)

v1 Dec. 2011 v2 Jan 16 2012: added comment regarding y-errors

nmmn.stats.gauss2d(par, varcov, n=10000)

Calculates random numbers drawn from the multinormal distribution in two dimensions. Computes also the probability associated with each number that can be used to computed confidence levels.

Arguments:

• par : array or list with structure [par0, par1, par2, …] with the best-fit parameters

• varcov : variance-covariance matrix of the parameters

• n : number of (a,b) points generated from the multivariate gaussian

Output:

• x,y : arrays of random values generated from the multinormal distribution

• prob : probability associated with each value

Usage: >>> x,y,prob=gauss2d(par,varcov,100000)

v1 Apr. 2012

nmmn.stats.gen_ts(y, erry, n, zeropad=True)

Given a time series (TS) with uncertainties on the signal, this will generate n new TS with y-values distributed according to the error bars.

Output will be a \(n \times { m{size}(t)}\) array. Each row of this array contains a simulated TS.

Parameters:

• y – array of y-values for time series (do not need to be in order)

• erry – array of 1-sigma errors on y-values

• n – number of Mock TS to generate

• zeropad – are y-values<0 not allowed? True will make any values<0 into 0

Returns:

n x size(t) array. Each row of this array contains a simulated TS

nmmn.stats.intscat(x, y, errx, erry, a, b)

Estimates the intrinsic scatter about the best-fit, taking into account the errors in X and Y and the “raw” scatter. Inspired by Pratt et al. 2009, A&A, 498, 361.

Usage:

>>> sd=intscat(x,y,errx,erry,a,b)

where

• x,y : X and Y data arrays

• errx, erry : standard deviations in X and Y

• a,b : slope and intercept of best-fit linear relation

Returns the float sd with the scatter about the best-fit.

v1 Apr 9th 2012

nmmn.stats.linboot(x, y, n)

Performs the usual linear regression with bootstrapping.

Usage:

>>> a,b=lincorr(x,y,10000)

performs 10000 bootstrapped fits on the arrays x and y.

Plot the best-fit with

>>> amed=np.median(a)
>>> bmed=np.median(b)
>>> plt.plot(x,y,'o')
>>> plt.plot(x,amed*x+bmed)

Parameters:

• x – array of x data values

• y – array of y data values

• n – number of bootstrapping resamples that will be generated

Returns:

arrays a and b, each element is a different bootstrapped fit

nmmn.stats.linregress_error(x, y)

Compute the uncertainties in the parameters A,B of the least-squares linear regression fit y=ax+b to the data (scipy.stats.linregress).

x,y assumed to be Numpy arrays. Returns the sequence sigma_a, sigma_b with the standard deviations in A and B.

nmmn.stats.mode(x, **kwargs)

Finds the mode of a distribution, i.e. the value where the PDF peaks.

Parameters:

x – input list/array with the distribution

nmmn.stats.p2sig(p)

Given the p-value Pnull (i.e. probability of the null hypothesis) below, evaluates the confidence level with which we can reject the hypothesis in standard deviations.

Inspired on prob2sig.nb.

Usage:

>>> s=p2sig(0.001)

nmmn.stats.predband(xd, yd, a, b, conf=0.95, x=None)

Calculates the prediction band of the linear regression model at the desired confidence level, using analytical methods.

Clarification of the difference between confidence and prediction bands: “The 2sigma confidence interval is 95% sure to contain the best-fit regression line. This is not the same as saying it will contain 95% of the data points. The prediction bands are further from the best-fit line than the confidence bands, a lot further if you have many data points. The 95% prediction interval is the area in which you expect 95% of all data points to fall.” (from http://graphpad.com/curvefit/linear_regression.htm)

Arguments:

• conf: desired confidence level, by default 0.95 (2 sigma)

• xd,yd: data arrays

• a,b: linear fit parameters as in y=ax+b

• x: (optional) array with x values to calculate the confidence band. If none is provided, will by default generate 100 points in the original x-range of the data.

Usage:

>>> lpb,upb,x=nemmen.predband(all.kp,all.lg,a,b,conf=0.95)
calculates the prediction bands for the given input arrays

>>> pylab.fill_between(x, lpb, upb, alpha=0.3, facecolor='gray')
plots a shaded area containing the prediction band  

Returns:

Sequence (lpb,upb,x) with the arrays holding the lower and upper confidence bands

corresponding to the [input] x array.

References:

1. Introduction to Simple Linear Regression, Gerard E. Dallal, Ph.D.

nmmn.stats.predband_linboot(x, a, b, n)

Computes information for plotting the prediction band (“bow tie” plot) around best-fit. Run this after running linboot below.

Usage:

Plots prediction band and best-fit given data x,y

>>> n=1000
>>> a,b=nmmn.stats.linboot(x,y,n)
>>> xMock,yBest,yStd=nmmn.stats.confband_linboot(x,a,b,n)
>>> plt.plot(x,y,'o')
>>> plt.plot(xMock,amed*xMock+bmed)
>>> plt.fill_between(xMock,yBest-yStd,yBest+yStd,alpha=0.3, facecolor='gray')           

Parameters:

• x – array of x data values

• a – array of slopes from bootstrapped fits

• b – array of intercepts from bootstrapped fits

• n – number of bootstrapping resamples that will be generated

Returns:

arrays x (mock x-values with same interval as data), corresponding best-fit values, yStd (prediction band)

nmmn.stats.predbandnl(xd, yd, fun, par, varcov, deg, conf=0.95, x=None)

Calculates the prediction band of a nonlinear model at the desired confidence level, using analytical methods.

Arguments:

• xd,yd: data arrays

• fun : function f(v) - the model - which returns a scalar. v is an array such that v[0]=x, v[i>0] = parameters of the model

• par : array or list with structure [par0, par1, par2, …] with the best-fit parameters that will be fed into fun

• varcov : variance-covariance matrix obtained from the nonlinear fit

• deg : number of free parameters in the model

• conf: desired confidence level, by default 0.95 (2 sigma)

• x: (optional) array with x values to calculate the confidence band. If none is provided, will by default generate 100 points in the original x-range of the data.

Usage:

>>> lpb,upb,x=nemmen.predbandnl(all.kp,all.lg,broken,bfit,bcov,4,conf=0.95)
calculates the prediction bands for the given input arrays

>>> pylab.fill_between(x, lpb, upb, alpha=0.3, facecolor='gray')
plots a shaded area containing the prediction band  

Returns:

Sequence (lpb,upb,x) with the arrays holding the lower and upper confidence bands

corresponding to the [input] x array.

References: 1. http://www.graphpad.com/faq/viewfaq.cfm?faq=1099, “How does Prism compute confidence and prediction bands for nonlinear regression?” 2. http://stats.stackexchange.com/questions/15423/how-to-compute-prediction-bands-for-non-linear-regression 3. see also my notebook)

nmmn.stats.r2(ydata, ymod)

Computes the “coefficient of determination” R^2. According to wikipedia, “It is the proportion of variability in a data set that is accounted for by the statistical model. It provides a measure of how well future outcomes are likely to be predicted by the model.”

This method was inspired by http://stackoverflow.com/questions/3460357/calculating-the-coefficient-of-determination-in-python

References: 1. http://en.wikipedia.org/wiki/Coefficient_of_determination 2. http://stackoverflow.com/questions/3460357/calculating-the-coefficient-of-determination-in-python

v1 Apr 18th 2012

nmmn.stats.r2p(r, n)

Given a value of the Pearson r coefficient, this method gives the corresponding p-value of the null hypothesis (i.e. no correlation).

Code copied from scipy.stats.pearsonr source.

Usage:

>>> p=r2p(r,n)

where ‘r’ is the Pearson coefficient and n is the number of data points.

Returns:

p-value of the null hypothesis.

nmmn.stats.random(a, b, n=None)

Generates an array of random uniformly distributed floats in the interval [x0,x1).

>>> random(0.3,0.4,1000)

nmmn.stats.randomvariate(pdf, n=1000, xmin=0, xmax=1)

Rejection method for random number generation: Uses the rejection method for generating random numbers derived from an arbitrary probability distribution. For reference, see Bevington’s book, page 84. Based on rejection*.py.

Usage:

>>> randomvariate(P,N,xmin,xmax)

where

Parameters:

• P – probability distribution function from which you want to generate random numbers

• N – desired number of random values

• xmin,xmax – range of random numbers desired

Returns:

the sequence (ran,ntrials) where ran : array of shape N with the random variates that follow the input P ntrials : number of trials the code needed to achieve N

Here is the algorithm:

• generate x’ in the desired range

• generate y’ between Pmin and Pmax (Pmax is the maximal value of your pdf)

• if y’<P(x’) accept x’, otherwise reject

• repeat until desired number is achieved

v1 Nov. 2011

nmmn.stats.redchisq(x, y, a=None, b=None, sd=None)

Returns the reduced chi-square error statistic for a linear fit:

chisq/nu

where nu is the number of degrees of freedom. If individual standard deviations (array sd) are supplied, then the chi-square error statistic is computed as the sum of squared errors divided by the standard deviations. See http://en.wikipedia.org/wiki/Goodness_of_fit for reference.

If a linear model is not provided via A,B (y=ax+b) then the method computes the chi-square using the best-fit line.

x,y,sd assumed to be Numpy arrays. a,b scalars. deg integer. Returns the float chisq/nu with the reduced chi-square statistic.

nmmn.stats.redchisqg(ydata, ymod, deg=2, sd=None)

Returns the reduced chi-square error statistic for an arbitrary model, chisq/nu, where nu is the number of degrees of freedom. If individual standard deviations (array sd) are supplied, then the chi-square error statistic is computed as the sum of squared errors divided by the standard deviations. See http://en.wikipedia.org/wiki/Goodness_of_fit for reference.

ydata,ymod,sd assumed to be Numpy arrays. deg integer.

Usage:

>>> chisq=redchisqg(ydata,ymod,n,sd)

where

• ydata : data

• ymod : model evaluated at the same x points as ydata

• n : number of free parameters in the model

• sd : uncertainties in ydata

nmmn.stats.redchisqxy(x, y, errx, erry, a, b)

Returns the reduced chi-square error statistic for a linear fit \(\chi^2/ u\) where nu is the number of degrees of freedom. The chi-square statistic is computed taking into account the errors in both X and Y (i.e. the effective variance). See equation 3 in Ascenso et al. 2012, A&A or Yee & Ellingson 2003 ApJ.

Usage:

>>> chisq=redchisqxy(xdata,ydata,errx,erry,a,b)

where

• xdata,ydata : data

• errx,erry : measurement uncertainties in the data

• a,b : slope and intercept of the best-fit linear regression model

nmmn.stats.residual(ydata, ymod)

Compute the residual sum of squares (RSS) also known as the sum of squared residuals (see http://en.wikipedia.org/wiki/Residual_sum_of_squares).

Usage:

>>> rss=residual(ydata,ymod)

where

ydata : data ymod : model evaluated at xdata

ydata,ymod assumed to be Numpy arrays. Returns the float rss with the mean deviation.

Dec. 2011

nmmn.stats.scatpratt(x, y, errx, erry, a, b)

This is an alternative way of computing the “raw” scatter about the best-fit linear relation in the presence of measurement errors, proposed by Pratt et al. 2009, A&A, 498, 361.

In the words of Cavagnolo et al. (2010): We have quantified the total scatter about the best-fit relation using a weighted estimate of the orthogonal distances to the best-fit line (see Pratt et al. 2009).

Usage:

sd=scatpratt(x,y,errx,erry,a,b)

Parameters:

• x,y – X and Y data arrays

• erry (errx,) – standard deviations in X and Y

• a,b – slope and intercept of best-fit linear relation

Return type:

float sd with the scatter about the best-fit.

v1 Mar 20 2012

nmmn.stats.scatterfit(x, y, a=None, b=None)

Compute the mean deviation of the data about the linear model given if A,B (y=ax+b) provided as arguments. Otherwise, compute the mean deviation about the best-fit line.

Parameters:

• x,y – assumed to be Numpy arrays.

• a,b – scalars.

Return type:

float sd with the mean deviation.

nmmn.stats.scatterfitg(ydata, ymod, deg)

Compute the mean deviation of the data about the model given in the array ymod, tabulated exactly like ydata.

Usage:

>>> sd=scatterfitg(ydata,ymod,n)

Parameters:

• ydata – data

• ymod – model evaluated at xdata

• n – number of free parameters in the model

Return type:

float sd with the mean deviation.

nmmn.stats.sig2conf(sig)

Given a number of std. deviations, translates it into a p-value. E.g., 1sigma -> p=0.683, 2sigma -> p=0.954, etc.

Inspired on p2sig method.

Usage:

>>> s=sig2conf(5.)

nmmn.stats.splitnorm(x, sig1=1.0, sig2=1.0, mu=0.0)

Split normal distribution (or asymmetric gaussian) PDF. Useful when dealing with asymmetric error bars.

See http://en.wikipedia.org/wiki/Split_normal_distribution.

Parameters:

• x – input array where the PDF will be computed

• sig1 – left standard deviation

• sig2 – right std. dev.

• mu – mode

Returns:

probability distribution function for the array x

class nmmn.stats.splitnorm_gen(momtype=1, a=None, b=None, xtol=1e-14, badvalue=None, name=None, longname=None, shapes=None, extradoc=None, seed=None)

Bases: rv_continuous

Split normal distribution defined using scipy.stats. Can be called as any scipy.stats distribution. I took the effort of defining the extra CDF and PPF methods below in order to speedup calls to this class (I have particularly in mind the package mcerp).

Parameters:

• x – input array where the PDF will be computed

• sig1 – left standard deviation

• sig2 – right std. dev.

• mu – mode

Examples:

Defines distribution with sig1=1, sig2=3, mu=0:

>>> split = splitnorm_gen(name='splitnorm', shapes='sig1, sig2, mu')
>>> s=split(1,3,0.0001)
>>> x=np.linspace(-10,10,100)

Computes PDF:

>>> s.pdf(x)

Computes CDF:

>>> s.cdf(x)

Generates 100 random numbers:

>>> s.rvs(100)

Warning

for some reason, this fails if mu=0.

nmmn.stats.splitstd(x)

Given the input distribution, this method computes two standard deviations: the left and right side spreads. This is especially useful if you are dealing with a split normal distribution from your data and you want to quantify the lower and upper error bars without having to fit a split normal distribution.

This is a quick nonparametric method, as opposed to the more computationally intensive minimization involved when fitting a function.

Algorithm:

• divide the original distribution in two distributions at the mode

• create two new distributions, which are the symmetrical versions of the left and right side of the original one

• compute the standard deviations for the new mirror distributions

Parameters:

x – array or list containing the distribution

Returns:

left.stddev, right.stddev

Note

do not forget to inspect x.

nmmn.finance module

Module contents

Miscellaneous modules for:

• astro: astronomy

• dsp: signal processing

• lsd: misc. operations on arrays, lists, dictionaries and sets

• stats: statistical methods

• plots: custom plots

• fermi: Fermi LAT analysis methods

• bayes: Bayesian tools for dealing with posterior distributions

• grmhd: tools for dealing with GRMHD numerical simulations

• finance: financial market

These are modules I wrote which I find useful – for whatever reason – in my research.